Je me propose de donner un éclairage aux débutants sur les principales mesures rencontrées en audio, afin d'être capable de lire et interpréter une réponse en fréquence, réponse impulsionnelle, waterfall, spectrogramme, etc.
Depuis la démocratisation de l'ordinateur domestique et d'outils logiciels très performants, la mesure audio s'est largement démocratisée et l'avènement d'Internet a conduit à la diffusion massive de toutes sortes de mesures.
Mais leur lecture et leur interprétation correcte ne se sont pas simplifiées pour autant et restent bien souvent très confuses; Les quelques notions présentées ici devraient permettre au débutant d'en éviter les principaux écueils.
Note: toutes les illustrations sont générées à l'aide de l'excellent REW.

La réponse en fréquence

La courbe la plus commune en audio et la plus simple est la courbe de réponse en fréquence. Elle permet de visualiser le niveau d'amplitude de la réponse d’un système (supposé linéaire), pour chaque fréquence contenue entre deux bornes. Elle devrait d'ailleurs plus logiquement être appelée "réponse en amplitude" ou "réponse amplitude / fréquence".
L'amplitude est le plus souvent indiquée sur l’axe vertical, en décibel (dB). Les fréquences sont représentées sur l’axe horizontal, en Hz ou kHz et le plus souvent en divisions logarithmiques.



Lorsqu’on « lit » une courbe de réponse en fréquence, il faut faire attention à quatre paramètres principaux :

• L’étendue de l’axe vertical : en principe aux alentours de 50dB soit 3 à 5dB par carreau, mais parfois on peut trouver plus de 100 voir 150dB en vertical, ce qui écrase complètement l’information et enjolive particulièrement la courbe qui devient bien régulière;


• Le lissage de la courbe : une mesure acoustique brute produit presque toujours des variations locales considérables de niveau (effet du filtrage en peigne causé par les réflexions sur les parois et obstacles du local) c’est pourquoi il peut être utile et judicieux de lisser la courbe en prenant une valeur moyenne par fraction d’octave (1/3, 1/6, 1/12, 1/24 d’octave sont couramment utilisées). Là encore, abuser du lissage peut conduire à une présentation enjolivant exagérément la courbe… (voir exemple ci-dessous à gauche). le lissage d’une réponse en fréquence devrait toujours être indiqué car il est presque toujours appliqué pour rendre la courbe lisible.


• Le fenêtrage temporel : c’est une méthode permettant de calculer la réponse un système « comme si » le mesure était faite en conditions anéchoïques, en restreignant la fenêtre temporelle d'analyse à la portion de signal se terminant avant les premières réflexions (avec pour inconvénient de réduire la bande de fréquence valide aux fréquences médium / aiguës). Le fenêtrage temporel appliqué pour calculer la réponse en fréquence devrait toujours être indiqué; quand il ne l'est pas on peut supposer qu'aucun fenêtrage n'est appliqué (beaucoup de logiciels d'analyse ne le permettent pas).


• Les bornes de l’échelle des fréquences : en principe de 20Hz à 20kHz pour l’audio, mais il peut être utile d’étendre ou de réduire cette plage. Attention également au type d’échelle adopté, le plus souvent logarithmique, ce qui signifie qu'une octave (un doublement de fréquence) occupe toujours le même espace le long de l'axe horizontal.

Ci-dessus la même mesure, présentée avec des échelles verticales et des lissages différents; deux paramètres qui peuvent (parfois à dessein) rendre délicate la lecture des courbes.

Interprétation de la réponse en fréquence

Pour interpréter correctement la courbe de réponse en fréquence lue, il faut connaître les conditions de mesure du système : Est-ce une mesure acoustique (avec un micro) ou électrique (en sortie d’un ampli ou d’un lecteur CD par exemple…) Si c’est une mesure acoustique, à quelle distance et dans quel axe par rapport au système ? Le cas échéant, quel est le fenêtrage temporel appliqué ? Etc. Les questions sont nombreuses et en faire le tour nécessiterait un livre entier...

Prenons néanmoins le cas le plus courant, celui de la réponse en fréquence d'un système mesurée à la position d'écoute. Tout d'abord pour être utilisable, la courbe devrait être lissée au 1/6eme d'octave, l'échelle verticale montrer 2 à 5dB par carreau (soit 50 à 60dB d'amplitude verticale), et l'échelle des fréquences couvrir la bande audio habituelle soit 20Hz-20kHz.

Les principaux critères d'analyse que l'on peut donner:

• La courbe ne devrait pas présenter de fortes variations "locales" telles celles visibles à 55, 75, 90, 200, 1600Hz sur l'exemple ci-dessus;
• Une certaine décroissance de la réponse dans l'aigu est normale; elle dépend de la distance enceinte / micro et aussi (surtout) du profil d'absorption de la pièce (dans le cas d'une mesure non fenêtrée).

Mais, contrairement à ce qu'on lit ici ou là, il est relativement illusoire de se référer à une "courbe-cible" prédéfinie, car de nombreux paramètres importants ne sont pas pris en compte:

• directivité de l'enceinte,
• caractéristiques acoustiques du local,
• distance d'écoute (de mesure);

Enfin une telle courbe-cible devrait dépendre (fortement...) du niveau SPL mesuré, afin de prendre en compte l'indispensable correction de volume physiologique.

Le RT60 ou "temps de réverbération"

Lorsqu'un son est émis dans un local fermé il se propage dans toutes les directions à partir de sa source et rencontre donc rapidement les parois, sur lesquelles il est réfléchi. Après de nombreux "rebonds" le son finit par être suffisamment atténué et s'éteint, ce phénomène est appelé "réverbération".
Le "RT60" est défini comme le temps nécessaire pour qu'un son soit atténué de 60dB, et devienne donc pratiquement inaudible.
La notion et la théorie qui l'entoure furent développées par W. Sabine dans le cadre de l'étude de l'acoustique des salles de concert, donc vastes (quelques centaines à quelques dizaines de milliers de m3). Son utilisation dans le cadre de l'audio domestique (quelques dizaines de m3) contrevient aux hypothèses de base (vrai champ 'diffus', source omnidirectionnelle, etc.) mais peut cependant être utile moyennant quelques précautions d'usage:

• Les valeurs mesurées sont très dépendantes des lieux et du protocole utilisés (type et position de la source, position du micro, modalités pratiques de calcul...) et donc difficilement comparables,
• La notion de RT60 ne s'applique pas au fréquences graves dans une petite pièce, le champ acoustique n'étant alors plus du tout de type diffus mais modal.

L'absorption du son par une paroi n'étant pas uniforme selon la fréquence, le RT60 ne se résume donc pas à une simple valeur numérique mais est représenté par une courbe temps / fréquence:


Cette courbe est généralement lissée à l'octave ou au 1/3 d'octave, selon le logiciel utilisé. L'ordre de grandeur constaté pour des pièce domestiques est d'une demi-seconde.
L'amplitude verticale du graphe ne devrait dont pas excéder 1 à 2s max. Pour l'axe des fréquences l'intervalle utile est 100/200 -> 10000Hz, la notion étant sans signification en dehors de cette plage.
Il faut également porter une attention particulière au mode de calcul utilisé par le logiciel, car la valeur affichée est le plus souvent issue d'une extrapolation: le rapport signal/bruit d'une mesure audio effectuée avec des moyens non spécialisés étant généralement insuffisant pour bien caractériser une décroissance de 60dB, le logiciel considère la portion initiale de la décroissance, soit les 10, 20 ou 30 "premiers" dB (on parle alors d'EDT "Early Decay Time", T20 ou T30). Hors cette portion initiale peut être affectée d'artefacts liés à des caractéristiques spécifiques de la pièce (volumes couplés, flutter écho, etc.); Une courbe de RT60 doit donc toujours être appréciée avec une certaine méfiance.
REW possède quant à lui un mode de calcul spécifique "Topt" qui n'est pas normalisé mais donne généralement les résultats les plus fiables.

Interprétation du RT60

Il n'y a pas de recette miracle pour définie un "bon" RT60 pour une salle d'écoute. Un critère fiable est cependant la constance de la valeur mesurée sur la bande la plus large possible; Les très mauvaises acoustiques présentent souvent un RT60 à profil "en cloche", avec un max centré vers 500Hz/1kHz soit la fréquence centrale du spectre audio et la plus critique pour l'intelligibilité de la voix.
Pour la valeur moyenne il est nécessaire de considérer en premier lieu le volume de la salle: si 0,5s est acceptable pour un très grand séjour, c'est une valeur bien trop élevée pour une écoute de qualité dans une chambre.
Le "type" d'écoute souhaité rentre aussi en compte: hyper précise de type "studio" ou très enveloppante, le RT60 visé sera différent comme les traitements acoustiques à mettre en oeuvre.

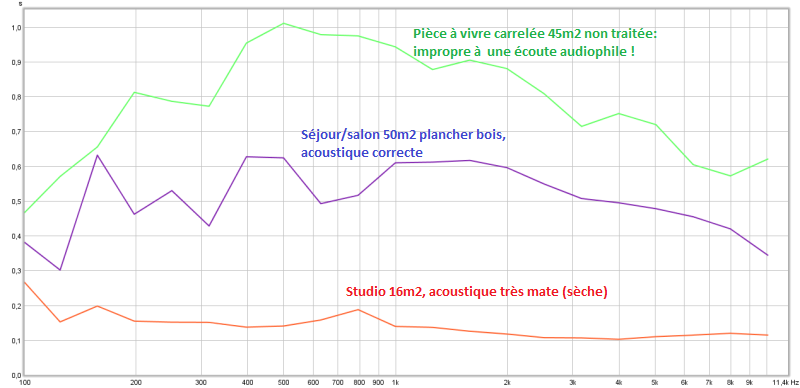
Courbe de RT60 mesurées dans 3 acoustiques très différentes.

La réponse impulsionnelle

La Réponse Impulsionnelle (RI) est définie comme la réponse d'un système (électrique ou mécanique) à une impulsion de Dirac. "Duale" de la réponse en fréquence, elle caractérise le comportement temporel du système en réponse à une excitation.
La RI s'utilise dans plusieurs cas de figure avec des modalités bien différentes, nous allons les passer en revue.
Tout d'abord, voici à quoi ressemble une impulsion de Dirac:
Il s'agit donc d'un signal représenté sous sa forme temporelle: l'axe des abscisses représente le temps en millisecondes (ici de -1 à 2.5ms environ), celui des ordonnées représente l'amplitude du signal (ici sous une forme normalisée en pourcentage de l'amplitude maximale atteinte).
Une fois échantillonné comme ici à 44.1 kHz, chaque point sur la courbe représente un sample distant de ses voisins de 1/44100 = 0.0227ms. On observe donc ici un signal constant d'amplitude nulle sauf en 1 point (en théorie l'amplitude en ce point serait infinie). La largeur du pic de l'impulsion caractérise la fréquence de coupure haute du système, ici deux points soit 44100/2=22050Hz.

Ainsi, voici la RI d'un filtre passe-bas à 5kHz: (et à titre d'information, ses réponse en fréquence et en phase)

On voit que l'impulsion "mesure" environ 8 points de large à sa base, soit 44100/8 ~ 5000Hz. On remarque aussi que cette impulsion est caractéristique d'un filtre dit "à phase linéaire" car elle est symétrique par rapport au point d'amplitude maximale. Un tel filtre ne déforme pas la phase, mais possède l'inconvénient de présenter des pré- et post- ondulations, dont l'amplitude et le nombre dépendent de la pente du filtre.

Voici ce qui se passe si l'on filtre en passe-haut cette impulsion, à 50Hz par exemple:


Si l'effet du passe-haut est parfaitement visible sur la réponse en fréquence, on constate en revanche que la RI est pratiquement indiscernable la précédente qui ne comportait pas de passe-haut.
Confirmation sur ce graphe regroupant les deux RIs:


Pour voir apparaitre clairement la différence entre les deux RI, il faudra modifier les échelles de tracé pour zoomer considérablement en amplitude:

Cette fois l'axe horizontal montre 30ms (contre 3 auparavant) et l'axe vertical 7% (contre 120% auparavant). L'ondulation caractéristique du passe-haut apparaît alors, avec une amplitude très faible (200 fois inférieure à celle du pic principal de l'impulsion) mais une durée significative (de l'ordre de de 20ms correspondant à la période de la fréquence de coupure 50hz, soit 100 fois plus large que le pic principal de l'impulsion). On met alors clairement en évidence le phénomène qui complique considérablement la lecture d'un graphe de réponse impulsionnelle:

Les représentations temporelles des phénomènes touchant le grave et l'aigu se passent à des échelles complètement différentes, empêchant leur bonne lisibilité sur un même graphique de RI.

Ainsi les phénomènes touchant le grave ont une amplitude beaucoup plus faible et une durée beaucoup plus longue que ceux touchant l'aigu (sur le plan théorique on remarquerait que les aires sont équivalentes).

Les RI d'enceinte acoustique sont souvent présentées sur une axe temporel couvrant quelques millisecondes: ceci permet de visualiser uniquement le comportement relatif au haut-médium / aigu.
Exemples:


Ces quatre RI correspondent à des enceintes acoustiques mesurées à 1m dans l'axe. Un oeil averti peut déduire de ces graphes quelques caractéristiques (topologie de filtrage, mise en phase, résonances...), mais cela restera très parcellaire; En particulier le raccord grave/médium sur une 3 voies est pratiquement "invisible" sur ce type de représentation.
La réponse à l'échelon (step response) apporte un éclairage complémentaire.

La RI caractérise également un local d'écoute. Dans ce cas on passe à un autre type de représentation avec une échelle de temps beaucoup plus étendue (de l'ordre de la seconde) et un axe verticale représentant l'amplitude en dB.


Ce type de représentation permet de visualiser la décroissance du son dans la pièce et notamment l'intensité des premières réflexions par rapport au signal initial dont l'amplitude est par convention fixée à 0dB.

La réponse à l'escalier ou "step response"

Elle représente la réponse d'un système à un signal ayant la forme d'une marche d'escalier:


L'avantage de ce type d'excitation par rapport à la réponse impulsionnelle est que les fréquences graves y sont présentes avec une amplitude comparable à celle des fréquences aiguës; Ainsi les deux phénomènes peuvent s'appréhender plus facilement sur le même graphe, par exemple la réponse ci-dessous est celle correspondant à la deuxième des enceintes présentées plus haut.


On y reconnaît plus facilement une enceinte 3 voies.

La réponse en phase, le délai de groupe

Avec la réponse en amplitude, la réponse en phase est le deuxième volet de la représentation fréquentielle d'un système. Elle sont d'ailleurs le plus souvent représentées sur le même graphe, comme dans l'exemple ci-dessous:


Lorsqu'un signal traverse un système, ses composantes fréquentielles sont décalées temporellement car elles sont plus ou moins retardées par l'effet des différents filtres composant le système. Ce phénomène peut être représenté sous la forme d'un angle de phase affectant chaque fréquence restituée, la référence 0° étant généralement fixée à la fréquence de coupure haute du système.

La première difficulté dans la représentation de la phase est qu'un angle varie par convention sur un intervalle de 360° (-180 à -180 par exemple) alors que la phase d'un système peut présenter une variation considérablement plus grande; ce qui entraîne une représentation dite "repliée" comme dans l'exemple ci-dessus.
La même courbe de phase représentée "dépliée" montre une variation sur plus de 1000°:


La deuxième difficulté réside dans la méthode de calcul de la phase mise en oeuvre dans les logiciels de calcul audio. Ce calcul nécessite une référence temporelle (un point "zéro" d'origine des temps) dont le placement a des répercussions fondamentales sur la phase calculée. Ce point est le plus souvent placé à l'abscisse correspondant au maximum en amplitude de la RI, ce qui donne en principe une courbe de phase dont le 0° est situé à la fréquence de coupure haute du système (mais ce n'est pas obligatoire).
REW offre la possibilité de recaler le point d'origine temporelle, voici un exemple de l'effet produit:
Sur l'IR ci-dessus la référence temporelle a été placée automatiquement par REW sur le premier pic de l'IR, qui ne correspond pas au maximum d'amplitude.

Une fois la référence temporelle recalée automatiquement par REW (fonction "Estimate IR delay", notez la nouvelle position de l'origine des temps), voici la courbe de phase calculée:

L'allure de la courbe de phase change complètement ! Mais on peut remarquer que le point Oms a été positionné par REW sur le pic d'amplitude négatif, ce qui n'est pas encore tout à fait ce qu'on attend.
Heureusement il reste la possibilité de décaler manuellement le point 0 pour le positionner sur le pic positif:

Cette fois l'allure de la courbe de phase correspond à ce qui est attendu avec un minimum correspondant aux fréquences les plus hautes reproduites.

La troisième difficulté réside dans la notion même de phase appliquée à un système dans lequel des réflexions "tardives" (décalées de plus d'une période) interviennent de façon non négligeable; ce qui est le cas d'une mesure acoustique effectuée dans un local domestique. La notion de phase ne s'applique alors correctement que sur un signal fenêtré temporellement de façon à éliminer virtuellement ces réflexions, ce qui restreint considérablement le domaine de validité en fréquence.

De la même façon que la phase le délai de groupe représente le retard des composantes fréquentielles du signal sous forme d'un temps exprimé en secondes (ou millisecondes). Selon les cas l'une ou l'autre représentation peut être préférée, mais l'information contenue est équivalente.
Exemple de courbe de délai de groupe:

On retrouve sur cette courbe 3 points d'inflexions à 350, 900 et 2900Hz visibles également sur les courbes de phase montrées plus haut.

Le waterfall ou "diagramme en chute d'eau"

Ce type de représentation en 3 dimensions permet de visualiser globalement les comportements temporel et fréquentiel du système. Il est très utile notamment pour analyser les modes propres d'une pièce, comme dans l'exemple ci-dessous:

On voit bien que le comportement de la pièce dans les fréquences graves est dominé par les deux modes propres 27 et 57Hz, tandis que les modes se resserrent ensuite (78, 90, 121, 139Hz...).
Deux paramètres d'analyse sont très importants dans ce type de visualisation:

• La fenêtre temporelle d'analyse, qui en détermine la résolution en fréquence. Dans notre exemple la fenêtre est de 200ms ce qui donne une résolution de 5Hz, ce qui veut dire que deux modes séparés de moins de 5Hz seront indiscernables à l'affichage (de même que la résolution temporelle sera de 200ms).
• L'intervalle de temps affiché, ici de 600ms.

Ces deux paramètre déterminent la plage de fréquences pour lesquelles le graphe est valide. Si l'on souhaite par exemple visualiser le comportement d'une enceinte dans le médium-aigu, la fenêtre temporelle d'analyse ne devra pas excéder 5 à 10ms, ce qui entraîne une résolution fréquentielle de 100 à 200Hz.

Dans tous les cas la plage de fréquences affichées ne devrait pas excéder une décade (soit fmax = 10*fmin) afin de conserver sa cohérence; le spectre audio complet s'étalant sur 3 décades.

Le sonogramme

Le sonogramme (également appelé spectrogramme) est une représentation en 3 dimensions tout à fait comparable au waterfall, la différence étant que l'amplitude est représentée sous la forme d'un dégradé de couleurs.
Voici par exemple le sonogramme correspondant au waterfall grave affiché plus haut:

On retrouve précisément les modes propres cités plus haut (27, 57, 90, 121, 139...).

Malgré sa moindre précision en amplitude, le sonogramme est utile car il fait apparaître plus facilement que le waterfall les phénomènes complexes de nature temporelle comme les annulations et les irrégularités de délai de groupe:

Ce sonogramme représente la même mesure que précédemment, mais affichée avec une fenêtre d'analyse de 50ms. Il permet de distinguer le signal direct de la réflexion qui parvient à l'auditeur environ 35ms plus tard (correspondant à un aller-retour dans une pièce de 5m de long) mais avec un niveau plus élevé, compromettant la qualité de restitution de l'extrême-grave.

La réponse aux signaux carrés

La réponse au signaux carrés était le domaine de prédilection de l'oscilloscope, car le signal d'excitation périodique est le seul compatible avec le mode de fonctionnement de ce type d'appareil (initialement analogique). Pour l'analyse de systèmes acoustiques il ne présente que très peu d'intérêt mais on le rencontre malgré tout de temps en temps utilisé à titre d'illustration de la réponse en phase d'un système.
C'est assez trompeur car un signal carré ne contient que les harmoniques impaires de sa fréquence de base; les caractéristiques détectables dans le graphe ne concernent donc que ces fréquences... à l'exclusion de toutes les autres.
Il est ainsi possible en choisissant adroitement la fréquence de base du carré, de masquer un mauvais comportement à la fréquence de croisement d'une enceinte multi-voie.
Par exmple, voici une série de réponses sur signaux carrés (partant du bas: 25, 50, 100, 200, 400, 800, 1600, 3200hz):

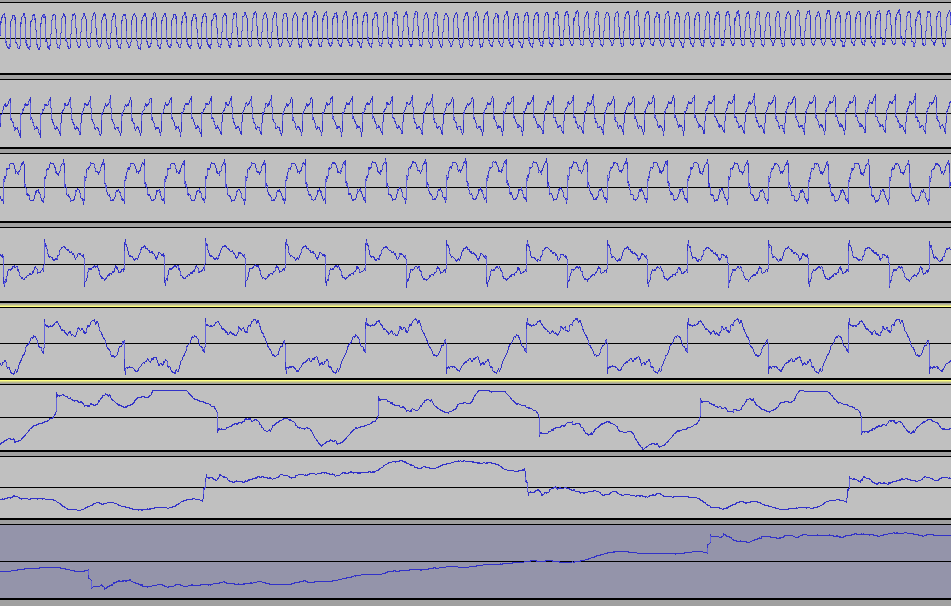
Présentés indépendamment, il serait bien difficile de déterminer si ils sont issus du même système, ce qui montre que ce type de graphe est peu représentatif du système mesuré. On notera par exemple le bon aspect (relatif) des 25 et 50Hz (2 premiers en partant du bas) par rapport au mauvais 400Hz (5eme en partant du bas).